372. BENEFACT – The
Benefactor
Another chapter of the municipal chronicles of a well
known unbelievable lordly major town (if this town is not well known to you,
you might want to solve problem CSTREET first) tells us the following story:
Once upon a time the citizens of the unbelievable
lordly major town decided to elect a major. At that time this was a very new
idea and election campaigns were completely unknown. But of course several
citizens wanted to become major and it didn't took long for them to find out,
that promising nice things that never will become real tends to be useful in
such a situation. One candidate to be elected as a major was Ivo sometimes
called the benefactor because of his valuable gifts to the unbelievably lordly
major towns citizens.
One day before the election day Ivo the benefactor
made a promise to the citizens of the town. In case of his victory in the
elections he would ensure that on one of the paved streets of the town street
lamps would be erected and that he would pay that with his own money. As
thrifty as the citizens of the unbelievable lordly major town were, they
elected him and one day after the elections they presented him their decision
which street should have street lamps. Of course they chose not only the longest
of all streets but renamed several streets so that a very long street in the
town existed.
Can you find how long this street was? To be more
specific, the situation is as follows. You are presented a list of all paved
streets in the unbelievable lordly major town. As you might remember from
problem CSTREET in the town the streets are paved in a way that between every
two points of interest in the town exactly one paved connection exists. Your
task is to find the longest distance that exists between any two places of
interest in the city.
Input. The first line contains the number of
testcases t. The first line of each test case contains the number of places n (2 ≤ n ≤ 50000) in the town. Each street is given at
one line by two places (1 ≤ a, b ≤ n) and the
length of the street (0 ≤ l <
20000).
Output. For each testcase output one line which
contains the maximum length of the longest street in the city.
|
Sample input |
Sample output |
|
1 6 1
2 3 2
3 4 2
6 2 6
4 6 6
5 5 |
12 |
РЕШЕНИЕ
графы – поиск в ширину
Задано
взвешенное дерево. Найдите в нем самый длинный путь.
Анализ
алгоритма
Кратчайший
путь на взвешенном дереве можно найти поиском в ширину (не обязательно
алгоритмом Дейкстры).
Запустим
поиск в ширину из первой вершины. Найдем вершину v, до которой путь наибольший.
Далее запустим поиск в ширину из вершины v и найдем вершину u, до
которой путь наибольший. Найденный
путь из v в u является самым длинным.
Пример
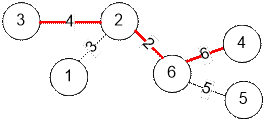
Реализация алгоритма
#include <cstdio>
#include <deque>
#include <vector>
#include <cstring>
#include <algorithm>
#define MAX 50001
#define INF 2100000000
using namespace std;
int i, j, n;
int b, e, dist, tests;
struct road
{
int v, dist;
road(int v, int dist) : v(v), dist(dist) {}
};
vector<vector<road>
> m;
deque<int> q;
int d[MAX];
int bfs(int v)
{
q.clear();
q.push_back(v);
while (!q.empty())
{
int v = q.front(); q.pop_front();
for (int i = 0; i < m[v].size(); i++)
{
int to = m[v][i].v;
if (d[to] == -1)
{
d[to] = d[v] + m[v][i].dist;
q.push_back(to);
}
}
}
return max_element(d + 1, d + n + 1) - d;
}
int main(void)
{
scanf("%d", &tests);
while (tests--)
{
scanf("%d", &n);
m.assign(n + 1, vector<road>());
for (i = 0; i < n - 1; i++)
{
scanf("%d %d %d", &b, &e, &dist);
m[b].push_back(road(e,
dist));
m[e].push_back(road(b,
dist));
}
memset(d, -1, sizeof(d)); d[1] = 0;
int v = bfs(1);
memset(d, -1, sizeof(d)); d[v] = 0;
v = bfs(v);
printf("%d\n", d[v]);
}
return 0;
}